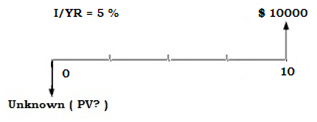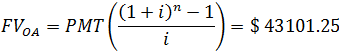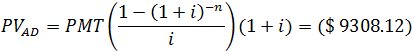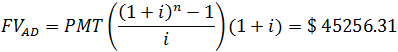Fear Not, It is not rocket science.
Once we grasp the meaning of the 5 components of TVM that is PV, FV, Payments (PMT), interest (i) and period (n), and with the help of the cash flow diagram (Check out HERE to understand what is a Cash Flow Diagram.), solving any TVM problems would be easy with the help of Excel function. In general, there are 6 basic types of TVM problems:
Present Value (PV) of a Single Sum
The TVM problem discounts a single future amount to a present value. A simple example would be: A bond will be worth $10,000 in 10 years. What should you pay for it today to earn 5% annually?
There are 4 components in play. We are given the future value FV of $10,000, the number of periods n is 10 years, and the interest, i at 5% per year. Unknown PV can be solved:
![]()
Future Value (FV) of a Single Sum
The TVM problem compounds a single amount to a future value. Here’s an example: What will $10,000 invested today for 5 years grow to be worth if compounded annually at 10% per year?
Again 4 known components are identified, we know the present value PV is ($10,000). It’s negative because it’s outflow of cash when we invested in an investment today. The number of period n is 5 years, and the interest i is 10%. We solved:
![]()
Present Value (PV) of an Ordinary Annuity
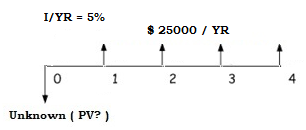
The problem discounts an annuity (of a series of equal payments) to a present value. An example of this type of time value of money problem: An insurance company is offering an annuity that pays $25,000 per year for the next 4 years. How much should you pay for the annuity to earn 5% per year?
Here we know that the payment PMT is $25,000 per year, with periods n being 4 years and the interest rate i is 5% per year. By solving:
![]()
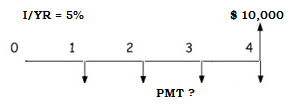
Future Value (FV) of an Ordinary Annuity
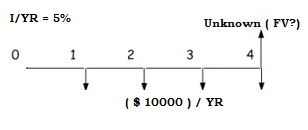
This TVM problem compounds an annuity to a future value. An example as follows: If you deposit $10,000 at the end of each year for 4 years, earning 5% annually, how much money will be in the account at the end of year 4?
Four known components are identified. The payment amount PMT is -$10,000 as we are depositing at the end of each year. The interest rate, i is 5% and the total periods n is 4 years. As we aren’t starting with anything, our present value is simply $0. We can easily solve for the future value:
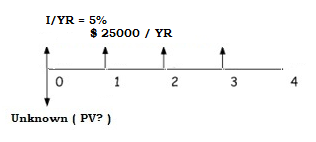
Present Value (PV) of an Annuity Due
This problem is common for calculating the present value of your future rent payments as specified in a lease you sign with your landlord in which we need to discount the formula one period forward as the payments are held for a lesser amount of time.
So when calculating the present value, we assume that the first payment was made today. Let’s take the same example of ordinary annuity earlier, it would give,
Thus giving payment PMT is $25,000 at the start of each year, with periods n being 4 years and the interest rate i is 5% per year. By solving:
Recall that the present value of an ordinary annuity returned a value of $8864.88. The present value of an ordinary annuity is less than that of an annuity due because the further back we discount a future payment, the lower its present value: each payment or cash flow in an ordinary annuity occur one period further into the future.
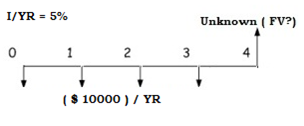
Future Value (FV) of an Annuity Due
When you are receiving or paying cash flows for an annuity due, payment in the series is made one period sooner, thus each amount is held longer at the end of the period. Take the earlier example and we have,
The payment amount PMT is -$10,000 but is deposited at the start of each year. The interest rate, i is 5% and the total periods n is 4 years. We can solve for the future value
Have you noted the difference between FV of an annuity due to that of ordinary annuity? It ends up higher as the amount was held longer which in favor of your deposits.
Other Types of TVM problems
The Amount needed to amortize a present value
This TVM problem determines a series of equal payments necessary to amortize a present value. An example: What are the yearly repayments on a 4-year loan of $10,000 at an annual rate of 5%?
In this problem, we are given the total number of periods, n of 4 years, a present value PV of $10,000, an annual interest rate, i of 5% and it is implied that the future value FV is $0. Thus we can solve:
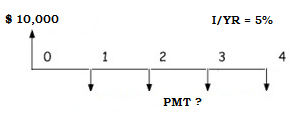
Payments needed to achieve a future value
This TVM problem compounds a series of equal payments into a future value. An example: At a 5% interest rate, how much needs to be deposited each year over the next 4 years to grow to $10,000?
The 4 known variables are the rate, i at 5%, the total number of periods, n which is 4 years, and future value FV we are trying to achieve is $10,000. Assuming payments occur at the start of each year, the equation will be, ![]()
However, if payments are to occur at the end of each year, that will give one less interest period where
Note how time factored to the TVM problems, whether payment was made before a period or at the end of a period matter. Although you might not notice a huge difference, but when the amount dealing is large, and over a long period, the compounding effect is significant!
A solid foundation for understanding time value of money will pay dividends for years to come.
Final Word
In solving TVM problems, it is important to note that both the number of periods and the rate of interest are to express consistently. Say the rate and the number of periods are both expressed in years, but if the payment frequency of a problem is expressed monthly, to not cause any conflict in the formula, you will need to do some conversion.
When we are dealing with loans, investment analysis, capital budgeting, and many other financial decisions, the TVM is impossible to ignore. Its concepts are the core of the valuation of personal finances. Thus to have a solid foundation for understanding the time value of money will pay dividends for years to come.
Would you like to learn more about TVM? Remember to download the FREE Time Value of Money Calculator HERE.